저는 언제나 처럼 간단하게 이게 어떤 개념인지만 짚고 넘어가겠습니다. 자세한 내용은 다른 학술 블로그들을 참조해 주세요! 그럼 이번 글에서는 Norm에 대한 개념을 간단하게 잡아 봅시다!

What is Norm?

Norm은 수학적으로 벡터 공간 또는 행렬에 있는 모든 벡터의 전체 크기, 길이를 의미합니다. 단순화를 위해 표준이 높을수록 행렬 또는 벡터의 값이 커집니다.

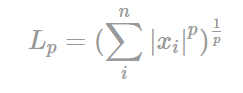
p: Norm의 차수(p의 차수에 따라 L0, L1, L2 결정)
N: 대상 벡터의 요소 수

L0 Norm

실제로 Norm은 아닙니다. 벡터의 0이 아닌 요소의 총 개수를 의미합니다. V(0,0) V(0,2)의 L0 Norm은 1입니다.

L1 Norm

Manhattan Distance또는 Taxicab Norm이라고 부르기도 하는 Norm입니다. 벡터 요소에 대한 절댓값의 합입니다. 벡터 사이의 거리를 측정합니다. 벡터의 모든 구성 요소에 대해서 동일한 가중치가 적용되어 계싼합니다. L1 Regularization, Computer Vision 영역에서 사용합니다.

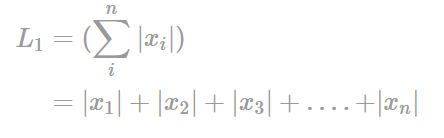
L1 Norm은 위와 같은 수식으로 표현 됩니다.

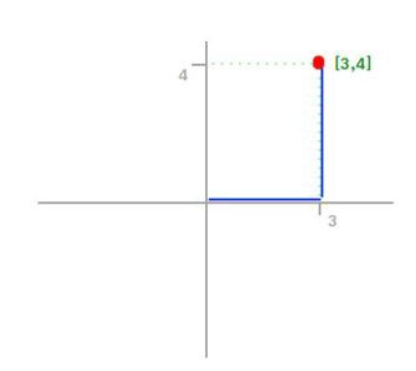
Vector X = [3, 4]: 7
출발지 원점(0, 0)에서 목적지 (3, 4)에 도착하기 위해 블록 사이를 여행하며 거리를 측정하는 방식입니다.

L2 Norm

Euclidean Norm이라도 부르는 가장 일반적인 Norm입니다. 한 지점에서 다른 지점으로 갈 때 가장 짧은 거리입니다.

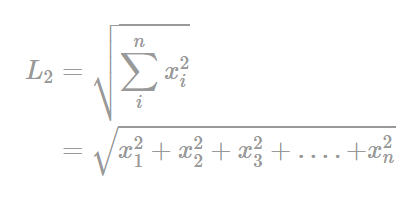
L2 Norm은 위와 같은 수식으로 표현 됩니다.

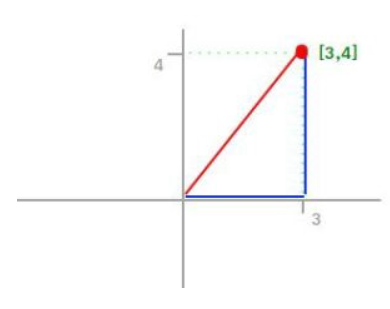
L2 Norm은 가장 직접적인 경로입니다. L2 Regularization, KNN, K-means 등의 알고리즘에서 사용됩니다. 벡터의 각 구성요소가 제곱된 형태이기 때문에 결과 값이 왜곡 될 가능성이 있기 때문에 고려해야합니다.

본 포스팅은 졸업작품을 위한 미팅 자료에 기반을 두고 있습니다. 팀원과 함께 진행하는 프로젝트입니다.